Introduction
Nothing beats the sweet reward of solving a sticky geometry question. In fact, every time I’ve given my class a challenging proof, the entire room would be abuzz. It is at times like this that I always suggest working in groups, as nothing quite compares to a hive mentality.
As it turns out, us math instructors aren’t the only ones solving geometric problems while buzzing around and annoying picnic-goers. For an example of geometric problem-solving and design, one need look no further than the common honey bee.

A Little Background
In 1998, a seven-year-old Dae was at the San Francisco Zoo, gawking over the Entomology exhibit. The honey bee habitat, a vertical honeycomb encased in plexiglass, was particularly captivating. “Why are they all the same shape?” “Is that on purpose?” “Do the bees know how to make them all hexagons?” Little did they know that Mathematicians, dating back to the Romans, pondered the same thing, possibly over some tea… with honey.
The Honeycomb Conjecture
The honeycomb conjecture, in shorthand terms, states that regular polygons “provide the least-perimeter way to enclose infinitely many unit areas in the plane.” (Source 1) Polygons with all-congruent sides (i.e. regular) will have a greater area than non-regular polygons with the same perimeter. Additionally, the perimeter of regular polygons is dependent on the number of sides. Regular polygons with the same area will see the perimeter and length of each side decrease as the number of sides increase, as shown in Figure 1.
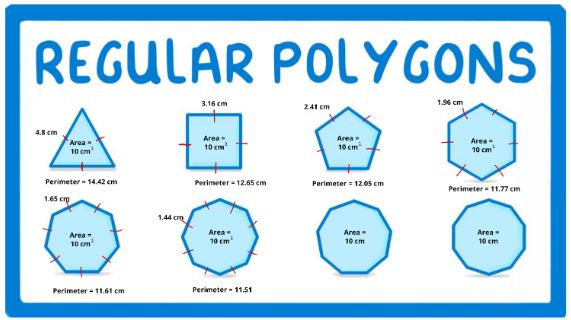
Beyond Bees
However, if one wants to build a continuous area from regular polygons, hexagons have the largest number of sides without resulting in any overlap. If one were to attempt the same interconnected structure with a heptagon or octagon, then the individual polygons would overlap, as seen in Figure 2.
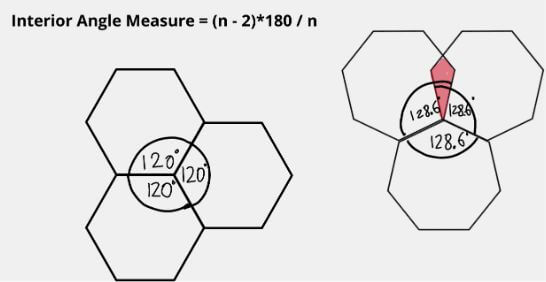
This continuous structure made up of congruent regular polygons is called a regular tessellation; the hexagonal tessellation provides the most structural integrity, forms the greatest amount of area, and does so with the least amount of material, when compared with other non-overlapping structures. Tessellations, where pressure is exerted over exponentially more sides, provide more structural support than a singular polygon structure. They can hold exponentially more weight without being warped or crushed. Egg cartons, inner layers of boxes, milk crates, and surgical mesh are all made with tessellations for this exact reason!
How Do Bees Know This?
So then, how do bees know to do this? How do bees know to build their honeycomb as a matrix of congruent regular hexagons? It turns out that Dr. Universe of Northwest Public Broadcasting was wondering the same thing, asking Sue Cobey, a bee researcher at Washington State University. The honeycomb-building process is actually a two-step process where “certain bees would start out making circles in the wax, using their body as a tool,” and for reasons unknown other bees “use their body heat to melt the wax from a circle shape into a hexagon shape.” (Source 2)
It could be an instinct formed through natural selection. It could be that they took correspondence geometry courses at Bee -YU. We may never know with absolute certainty how our pollinators know to do this, but frankly… it’s none of our beeswax. Inspired and ready to learn more? Connect with an amazing 1-on-1 Geometry Tutor now!
Sources:
- Hales Proves Hexagonal Honeycomb Conjecture
- Why Do Bees Make Hexagons in Their Hives?
- How Honeycombs Can Build Themselves

